playmath - 数学实验游乐场
软件简介
a-boy/playmath是一个数学实验游乐场!
- 2019-09-02 证明哥德巴赫猜想 https://nbviewer.jupyter.org/github/a-boy/playmath/blob/master/stage12-Goldbach%20Conjecture/stage12-try%20to%20prove%20Goldbach%20Conjecture.ipynb
Goldbach Conjecture Inequality 1 : gold(n)< prime_pi(n)+sigma(n,0)
gold(n): the min non-negative integer g makes that both n-g and n+g are
primes
prime_pi(n): the count of primes in 1..n
sigma(n,0): the count of n.divisors()
gold(n) < prime_pi(n), while n>344
gold(n) < prime_pi(n)*4395/3449751 ≈ prime_pi(n)*0.0013, while n>57989356
Goldbach Conjecture Inequality 2 : gold(n)< prime_pi(prime_pi(n)+n)
- 2019-10-28, 2019-11-17,解决3n+1问题
Collatz正奇数回归树生成规则(Collatz-Odd-Tree Generation Rule) :
- 每个节点的长子由
v(x)=(2*x-1)/3 or (4*x-1)/3产生 - 其余每个小兄弟由
h(x)=4*x+1迭代陆续产生 - x在完全的Collatz-Odd-Tree中是叶节点 iff (x%3==0)
证明3n+1猜想成立也就只需证明Collatz-Odd-Tree中逆向生成了所有的正奇数。 显然,从x0=1出发,通过 h(x)=4*x+1 和
v(x)=(2*x-1)/3 or (4*x-1)/3 反复迭代,会生成所有形如4k+1和4k-1的数,即所有正奇数。Collatz猜想证明完毕□
http://a-boy.tk/playmath/stage26-3n%2B1conjecture/[webgame]proving-3n+1-conjecture.html
- 2019-11-08 提出征服费马最后定理之 白鹤猜想 [a^n+b^n的互不相同质因数的乘积远远大于(a+b)]
- 2018-03-06, 证明孪生质数猜想 ,并提出更普遍的规律:任意质数阶差子序列如果出现了两遍就会继续出现无数遍,例如
{2},{4},{2*n},{6,6},{2,4,2},...... - 2010-02-04,发现 Prime-Gap-Inequality: The i-th prime gap
p[i+1]-p[i]<=i 馒头曲线 和 馒头模型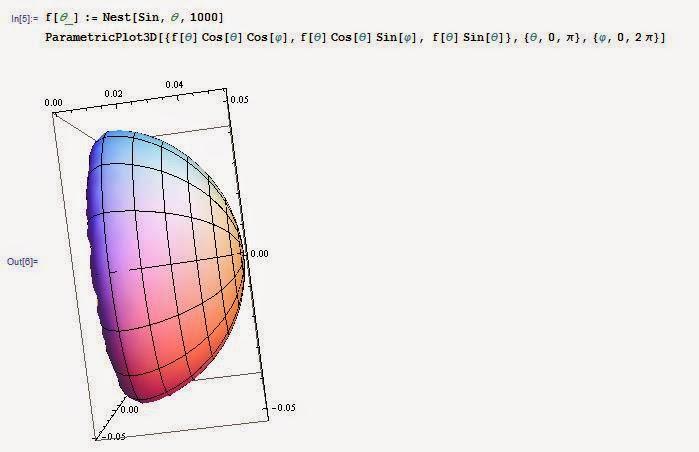
此外,playmath项目里有一个小巧实用的sagemath代码生成器 ,还有正在创作中的电子书 《 sagemath数学巡游 》、 《数论探索》…
采用sagemath作为主要的数学工具,你可以在Jupyter notebook或Jupyter
lab中浏览阅读.ipynb文档,但运行其中代码很可能需要sagemath函数库
